求正方形的面積
正方形的面積可以通過邊長的平方來計算,公式是:
\[ \text{面積} = \text{邊長}^2 \]
\[ \text{面積} = 16 \]
正方形的面積是 \(16\) 平方單位。
面積公式大全
面積是幾何學中一個重要的概念,它表示一個平面圖形所占據的空間大小。以下是一些常見幾何圖形的面積公式:
1. 矩形:
\[ \text{面積} = 長 \times 寬 \]
2. 正方形(一種特殊的矩形,長和寬相等):
\[ \text{面積} = 邊長 \times 邊長 \]
3. 三角形:
\[ \text{面積} = \frac{1}{2} \times 底 \times 高 \]
4. 平行四邊形:
\[ \text{面積} = 底 \times 高 \]
5. 梯形(等腰梯形或直角梯形):
\[ \text{面積} = \frac{1}{2} \times (上底 + 下底) \times 高 \]
6. 圓形:
\[ \text{面積} = \pi \times 半徑^2 \]
7. 扇形(圓的一部分):
\[ \text{面積} = \frac{1}{2} \times r^2 \times \theta \]
其中 \( r \) 是半徑,\( \theta \) 是圓心角的弧度數。
8. 橢圓:
\[ \text{面積} = \pi \times a \times b \]
其中 \( a \) 是半長軸,\( b \) 是半短軸。
9. 正多邊形(如正五邊形、正六邊形等):
\[ \text{面積} = \frac{1}{4} \times n \times a^2 \times \cot(\frac{\pi}{n}) \]
其中 \( n \) 是邊數,\( a \) 是邊長。
10. 弓形(圓的一部分,不包括扇形):
\[ \text{面積} = \frac{1}{2} \times r^2 \times (\theta_1 - \sin(\theta_1)) - \frac{1}{2} \times r^2 \times (\theta_2 - \sin(\theta_2)) \]
其中 \( r \) 是半徑,\( \theta_1 \) 和 \( \theta_2 \) 是弓形兩端的圓心角的弧度數。
11. 環形(大圓與小圓之間的區域):
\[ \text{面積} = \pi \times (R^2 - r^2) \]
其中 \( R \) 是大圓的半徑,\( r \) 是小圓的半徑。
12. 球冠(球體的一部分):
\[ \text{面積} = 2\pi rh \]
其中 \( r \) 是球體的半徑,\( h \) 是球冠的高度。
13. 圓柱體的側面積:
\[ \text{側面積} = 2\pi rh \]
其中 \( r \) 是底面半徑,\( h \) 是圓柱體的高度。
14. 圓錐體的側面積:
\[ \text{側面積} = \pi r l \]
其中 \( r \) 是底面半徑,\( l \) 是斜高。
這些是一些基本的面積計算公式,適用于不同的幾何形狀。
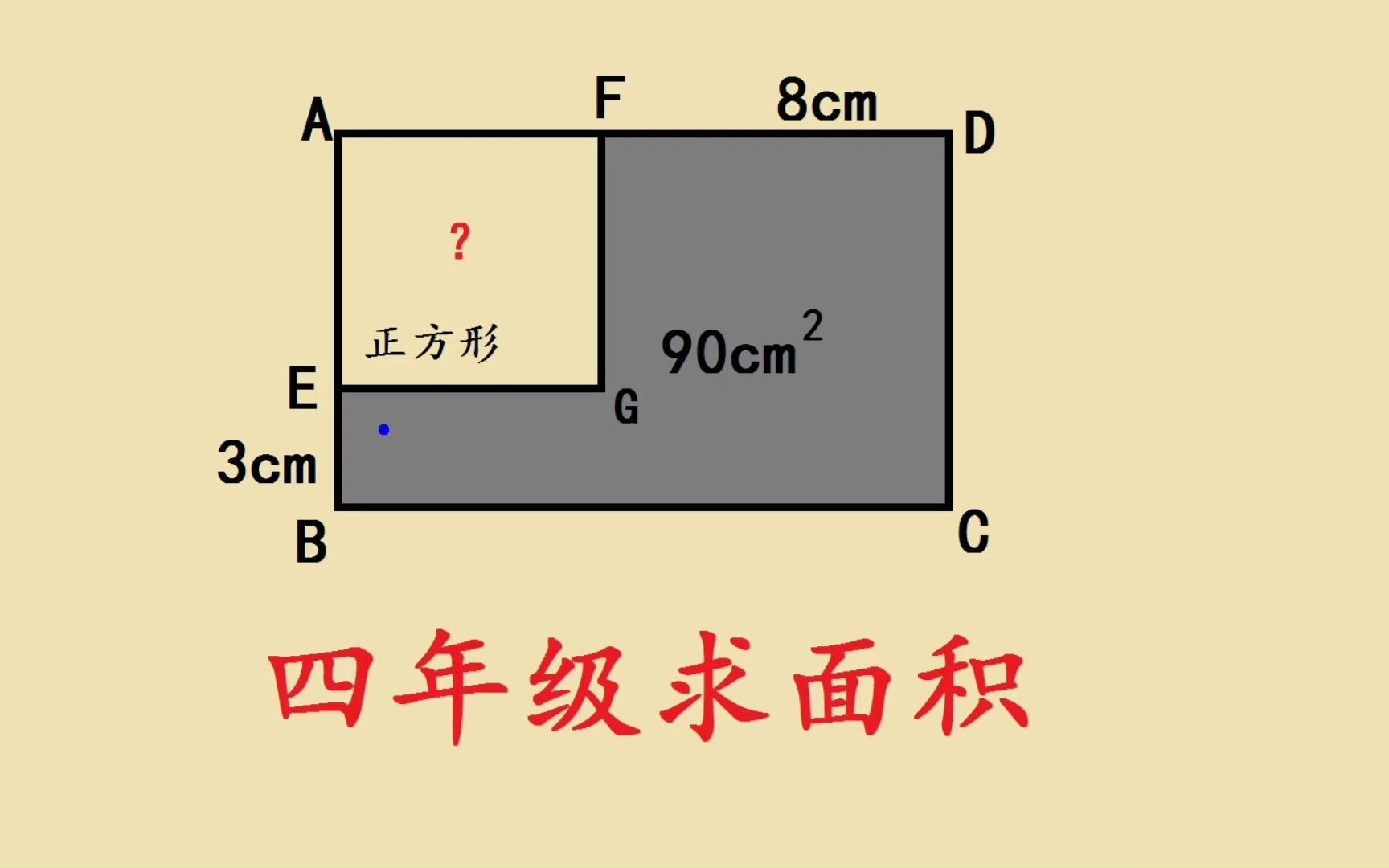
六年級求各種陰影圖形的
六年級數學中求陰影圖形的面積通常涉及到一些基本的幾何知識,比如三角形、矩形、圓形、梯形等的面積計算。以下是一些常見的陰影圖形面積計算方法:
1. 三角形:
- 底乘以高除以2,公式為:\[ \text{面積} = \frac{1}{2} \times \text{底} \times \text{高} \]
2. 矩形:
- 長乘以寬,公式為:\[ \text{面積} = \text{長} \times \text{寬} \]
3. 圓形:
- 半徑的平方乘以π,公式為:\[ \text{面積} = \pi \times r^2 \],其中 \( r \) 是圓的半徑。
4. 梯形:
- 上底加下底乘以高除以2,公式為:\[ \text{面積} = \frac{1}{2} \times (\text{上底} + \text{下底}) \times \text{高} \]
5. 扇形:
- 圓心角(以弧度為單位)乘以半徑的平方再乘以π然后除以360,公式為:\[ \text{面積} = \frac{\theta}{360} \times \pi \times r^2 \],其中 \( \theta \) 是圓心角的度數。
6. 組合圖形:
- 有時候陰影部分是幾個簡單圖形的組合,這時需要分別計算各個簡單圖形的面積,然后或者使用積分的方法(這通常超出六年級的范圍)。
如果你有具體的陰影圖形和數據,可以提供給我,我可以幫你計算具體的面積。

 微信掃一掃打賞
微信掃一掃打賞