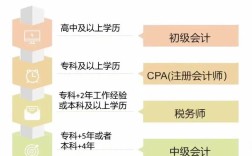
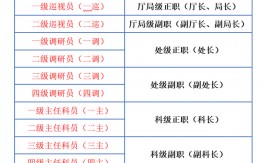
微積分是高中還是大學
微積分通常在大學階段作為數學專業的基礎課程之一進行學習。不過,一些高中的高級課程或數學競賽課程中也會涉及微積分的基本概念和簡單應用。在大學,微積分是理工科專業學生必須掌握的重要數學工具,它包括極限、導數、積分等概念。

微積分題目及答案
微積分是數學中的一個重要分支,它包括兩個主要的部分:微分學和積分學。微分學研究的是函數的局部變化率,而積分學研究的是函數在某個區間上的累積總和。這里有一些基礎的微積分題目和它們的答案:
1. 題目:求函數 \(f(x) = x^2\) 在 \(x = 2\) 處的導數。
答案:\(f'(x) = 2x\),所以 \(f'(2) = 2 \times 2 = 4\)。
2. 題目:計算定積分 \(\int_{0}^{1} x^2 dx\)。
答案:使用基本積分公式 \(\int x^n dx = \frac{x^{n+1}}{n+1} + C\),其中 \(n \neq -1\),我們得到 \(\int_{0}^{1} x^2 dx = \left[\frac{x^3}{3}\right]_{0}^{1} = \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3}\)。
3. 題目:求函數 \(g(x) = \sin(x)\) 的不定積分。
答案:\(\int \sin(x) dx = -\cos(x) + C\),其中 \(C\) 是積分常數。
4. 題目:計算極限 \(\lim_{x \to 0} \frac{\sin(x)}{x}\)。
答案:這個極限是著名的極限之一,其值為 1。可以通過洛必達法則或者幾何方法來證明。
5. 題目:求函數 \(f(x) = e^x\) 的導數。
答案:\(f'(x) = e^x\)。\(e^x\) 是其自身的導數。
6. 題目:計算二重積分 \(\iint_D x^2 y dA\),其中 \(D\) 是由 \(x = 0\), \(y = 0\), \(x = 1\), \(y = x\) 圍成的區域。
答案:首先確定積分區域,然后使用直角坐標系或極坐標系進行積分。在這個例子中,我們可以使用直角坐標系,積分區域 \(D\) 可以表示為 \(0 \leq x \leq 1\), \(0 \leq y \leq x\)。\(\iint_D x^2 y dA = \int_{0}^{1} \int_{0}^{x} x^2 y dy dx\)。
這些只是微積分中的一些基礎題目。如果你有具體的微積分問題或者需要更復雜的題目和答案,隨時可以問我!
學完微積分秒殺高中數學
微積分是高等數學的一個重要分支,它包括了極限、導數、積分等概念。雖然微積分中的一些思想和方法可以幫助理解高中數學中的某些問題,但微積分本身并不能直接“秒殺”高中數學。
高中數學是一個廣泛的領域,包括但不限于代數、幾何、三角學、概率統計等。微積分只是其中的一部分,雖然它在解決某些問題時非常有用,但高中數學的其他部分仍然需要通過相應的學習來掌握。
例如,高中數學中的代數問題可能需要你熟練掌握方程和不等式的解法,幾何問題可能需要你理解圖形的性質和證明方法,而概率統計則需要你掌握數據分析和解釋的技能。
如果你已經學習了微積分,那么在處理一些高中數學問題時,你可能會有更多的工具和視角。但是,為了全面掌握高中數學,仍然需要系統地學習各個部分的內容。高中數學的考試通常也會涵蓋多個領域,因此僅僅依靠微積分是不夠的。

 微信掃一掃打賞
微信掃一掃打賞